Tochio's Computation on the Soroban/Mono-Division
MONO-DIVISION.
Remember the following tables:—
First Division—(Division by 1).
| 1 is once. | 2 is twice. | 3 is thrice. | 4 is 4 times. | 5 is 5 times. |
| 6 is 6 times. | 7 is 7 times. | 8 is 8 times. | 9 is 9 times. |
Note.—The above table is never used in mono-division, since the quotient of a number divided by 1 is the number itself. But its use will be found in poly-division as we shall subsequently see.
Second Division (Division by 2).
| (1/2) | 2nd part (of) I make 5. Read 2nd part 1 make 5. |
| 2 is once. 4 is twice, 6 is thrice, 8 is 4 times. |
Third Division (Division by 3).
| (1/3) | 3rd part (of) 1, make 3 & (suffix) 1. Read 3rd part 1, make 8 & 1. |
| (2/3) | 3rd part (of) 2, make 6 & (suffix) 2. Read 3rd part 2, make 6 & 2. |
| 3 is once. 6 is twice, 9 is thrice. |
Fourth Division (Division by 4).
| (1/4) | 4th part (of) 1, make 2 & (suffix) 2. Read as above. |
| (2/4) | 4th part„ (of)„ 2, make„ 5. |
| (3/4) | 4th part„ (of)„ 3, make„ 7 & (suffix) 2. Read„ as„ above„ |
| 4 is once. | |
| 8 is„ twice. |
Fifth Division (Division by 5).
| (1/5) | 5th part (of) 1, double 1. Read 5th part 1, double 1. |
| (2/5) | 5th„ part„ (of)„ 2, double„ 2. Read„ 5th„ part„ 2, double„ 2. |
| (3/5) | 5th„ part„ (of)„ 3, double„ 3. Read„ 5th„ part„ 3, double„ 3. |
| (4/5) | 5th„ part„ (of)„ 4, double„ 4. Read„ 5th„ part„ 4, double„ 4. |
| 5 is once. |
Sixth Division (Division by 6).
| (1/6) | 6th part (of) 1, subjoin 4. Read omitting (of) in operation. |
| (2/6) | 6th part (of) 2, make 3 & (suffix) 2. |
| (3/6) | 6th„ part„ (of)„ 3, make„ 5. |
| (4/6) | 6th„ part„ (of)„ 4, make„ 6 & (suffix) 4. |
| (5/6) | 6th„ part„ (of)„ 5, make„ 8 & (suffix)„ 2. |
| 6 is once. |
Seventh Division (Division by 7).
| (1/7) | 7th part (of) 1, subjoin 3. |
| (2/7) | 7th„ part„ (of)„ 2, subjoin„ 6. |
| (3/7) | 7th„ part„ (of)„ 3, make 4 & (suffix) 2. |
| (4/7) | 7th„ part„ (of)„ 4, make„ 5 & (suffix)„ 5. |
| (5/7) | 7th„ part„ (of)„ 5, make„ 7 & (suffix)„ 1. |
| (6/7) | 7th„ part„ (of)„ 6, make„ 8 & (suffix)„ 4. |
| 7 is once. |
Eighth Division (Division by 8).
| (1/8) | 8th part (of) 1, subjoin 2. |
| (2/8) | 8th„ part„ (of)„ 2, subjoin„ 4. |
| (3/8) | 8th„ part„ (of)„ 3, subjoin„ 6. |
| (4/8) | 8th„ part„ (of)„ 4, make 5. |
| (5/8) | 8th„ part„ (of)„ 5, make„ 6 & (suffix) 2. |
| (6/8) | 8th„ part„ (of)„ 6, make„ 7 & (suffix)„ 4. |
| (7/8) | 8th„ part„ (of)„ 7, make„ 8 & (suffix)„ 6. |
| 8 is once. |
Ninth Division (Division by 9) .
| (1/9) | 9th part (of) 1, subjoin 1. |
| (2/9) | 9th„ part„ (of)„ 2, subjoin„ 2. |
| (3/9) | 9th„ part„ (of)„ 3, subjoin„ 3. |
| (4/9) | 9th„ part„ (of)„ 4, subjoin„ 4. |
| (5/9) | 9th„ part„ (of)„ 5, subjoin„ 5. |
| (6/9) | 9th„ part„ (of)„ 6, subjoin„ 6. |
| (7/9) | 9th„ part„ (of)„ 7, subjoin„ 7. |
| (8/9) | 9th„ part„ (of)„ 8, subjoin„ 8. |
| 9 is once. |
Note—In operation, the words in parenthesis in the above tables should be omitted.
The author at first prepared the division tables in fractions, for instance: 1/2 makes 5, 1/3rd makes 3 & 1, 2/3rds make 6 & 2, 1/4th make 2 & 2, 2/4ths make 5, 3/4ths make 7 & 2, etc. However, it was thought convenient in practice to read the Indicator first, so the above form was taken; but, fractions are also given in parenthesis on the left, and it is left to learners to read them in either way liked.
The word "make" was selected to distinguish the operation from that of "once, twice, thrice," etc. But, if one understands the distinction, the word "be" may be substituted, if desirable.
Remember.—Whenever we say "once, twice, thrice," etc., the dividend in the original column is cleared and 1, 2, 3, etc., is respectively placed in the column ahead. Whenever we say "Make——&suffix——," the original column is transformed to the first figure and the suffix figure is inserted, or added to the following column. When there is no suffix, the original dividend column only is changed.
"Subjoin——" means that the original dividend column undergoes no change but "——" is added to the following column.
Remark.—To a learner, the foregoing tables may seem to be a puzzle, and very hard to remember. But, if you know that they are all based on 10, or if you consider the dividend figure as being one order higher, the tables are easily recollected. For instance:—
In "2nd part 1 make 5," consider 1 as 10 and divide by 2, then the quotient is 5. In "3rd part 1 make 3 and 1," divide 10 by 3 and the quotient is 3 and fractional 1. In "3rd part 2 make 6 and 2," divide 20 by 3, and you get 6 and fractional 2. In "5th part 1 double 1," in which the 1 is doubled and made 2, divide 10 by 5, and it is evidently 2. In "6th part 1 subjoin 4," you will see that 10 ÷ 6 is equal to 1 and fractional 4; and all the other tables may be similarly analysed. When we say "once, twice, etc.," each shows how many times the divisor is contained in the dividend.
Rule 5.—Division.—Place dividend on the right and divisor on the left, and divide from the highest column.
Let us now see how the Division tables work.
No. 1.—Indicator.—The first figure, or the highest column, of the divisor is called the Indicator, because it denotes the relative division table.
In mono-division, the divisor itself is the indicator.
123456789 ÷ 2 = 61728394.1/2
Fig. 14.

| A.—2nd part 1 make 5 — make the column into 5 | 523456789 |
| B.—2 is once — clear the column and insert 1 in the preceding column | 603456789 |
| C.— 2 is once; 2nd pt. 1 make 5 — take 2 from the column and carry forward 1; clear the remaining 1 and make the column 5 | 61456789 |
| D.—4 is twice — operate like B but carry forward 2 | 617056789 |
| E.—4 is twice; 2nd pt. 1 make 5 — operate like C but carry forward 2 | 617256789 |
| F.—6 is thrice—operate like B but forward 3 | 617280789 |
| G.—6 is thrice; 2nd pt. 1 make 5 — operate like C but forward 3 | 617283589 |
| H.—8 is 4 times—operate like B but forward 4 | 617283909 |
| I.—8 is 4 times—take 8 from the column and forward 4 into the preceding column, but do not divide the remainder 1 | 617283941 |
Note.—If you divide the remainder 1 saying 2nd pt. 1 make 5, it will be decimal 5.
123456789 ÷ 3 = 41152263.
Fig. 15.

| A.—3rd pt. 1 make 3 and 1—make the column 3 and add 1 in the posterior column | 333456789 |
| B.—3 is once—clear the column and forward 1 | 403456789 |
| C.—3 is once—operate as in B | 410456789 |
| D.—3 is once; 3rd pt. 1 make 3 and 1—take 3 off the column and forward 1; treat the remaining 1 as in A | 41136789 |
| E.—6 is twice—as in C but forward 2 | 411506789 |
| F.—6 is twice | 411520789 |
| G.—6 is twice; 3rd pt. 1 make 3 and 1 — take 6 and forward 2; treat the remaining 1 as in A | 411522399 |
| H.—9 is thrice—as in C but forward 3 | 411522609 |
| I.—9 is thrice | 411622683 |
123456789 ÷ 4 = 30864197.1/4
Fig. 16.
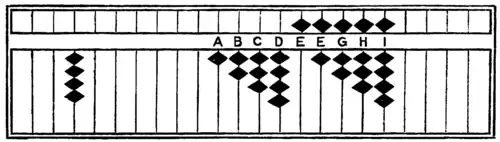
| A.—4th pt. 1 make 2 and 2—make the column 2 and insert 2 in the next column | 243456789 |
| B.—4 is once—clear the column and forward 1 | 303456789 |
| C.—4th pt. 3 make 7 and 2 — make the column 7 and add 2 in next column | 307656789 |
| D.—4 is once; 4th pt. 2 make 5 — take 4 and forward 1; make the column 5 | 308556789 |
| E.—4 is once; 4th pt. 1 make 2 and 2 — take 4 and forward 1; treat the remaining 1 as in A | 308623789 |
| F.—8 is twice — clear the column and forward 2 | 308640789 |
| G.—4 is once; 4th pt. 3 make 7 and 2—take 4 and forward 1; treat 3 as in C | 3086417(8+2)9 |
| H.—8 is twice; 4th pt. 2 make 5—take 8 and forward 2; make the column 5 | 308641989 |
| I.—8 is twice — take 8 and forward 2. 1 is a remainder | 308641971 |
Note.—If you continue division-saying 4th pt. 1 make 2 and 2; 4th pt. 2 make 5-decimal 25 is obtained.
123456789 ÷ 5 = 24691357.4/5
Fig. 17.

| A.—5th pt. 1 double 1—double 1 making the column 2 | 223456789 |
| B.—5th pt. 2 double 2—make the column 4 | 243456789 |
| C.—5th pt. 3 double 3—make the column 6 | 246456789 |
| D.—5th pt. 4 double 4—make the column 8 | 248856789 |
| E.—5 is once—clear the column and forward 1 | 246906789 |
| F.—5 is once; 5th pt. 1 double 1—as in E and A | 246912789 |
| G.—5 is once; 5th pt. 2 double 2—as in E and B | 246913489 |
| H.—5 is once; 5th pt. 3 double 3—as in E and C | 246913569 |
| I.—5 is once—take 5 and forward 1 | 246913574 |
Note.—If you divide 4—saying 5th pt. 4 double 4, you obtain decimal 8.
123456789 ÷ 6 = 20576131.3/6
Fig. 18.

| A.—6th pt. 1 subjoin 4—the column is not touched but 4 is added to the next column | 163456789 |
| B.—6 is once | 203456789 |
| C.—6th pt. 3 make 5 | 205456789 |
| D.—6th pt. 4 make 6 and 4 | 205896789 |
| E.—6 is once; 6th pt. 3 make 5 | 205756789 |
| F.—6 is once | 205706789 |
| G.—6 is once; 6th pt. 1 subjoin 4 | 2057611 (8+4)9 |
| In the first operation in the next column, take 2 which make 6 together with the subjoined 4, and 1 is forwarded. | |
| H.—6 is once; 6 is once | 205761309 |
| I.—6 is once | 20576131.3 |
Note—If you divide the remainder 3, decimal 5 is obtained.
123456789 ÷ 7 = 17636684.1/7
Fig. 19.
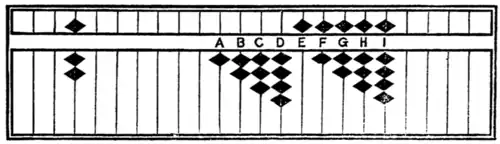
| A.—7th pt. 1, subjoin 3 | 153456789 |
| B.—7th pt. 5, make 7 and 1 | 171456789 |
| C.—7th pt. 4, make 5 and 5 | 175956789 |
| D.—7 is once; 7th pt. 2 subjoin 6 | 1762(5+6)6789 |
| E.—7 is once; 7th pt. 4 make 5 and 5 | 17685(6+5)789 |
| F.—7 is once; 7th pt. 4 make 5 and 5 | 176856(7+5)89 |
| G.—7 is once; 7th pt. 5 make 7 and 1 | 176366799 |
| H.—7 is once; 7th pt. 2 subjoin 6 | 1768566829(+6) |
| I.—7 is once; 7 is once | 1763666841 |
Where unoperated parts appear in parenthesis, the remark under G, Fig. 18, will similarly apply.
123456789 ÷ 8 = 15432098.5/8
Fig. 20.

| A.—8th pt. 1 subjoin 2 | 143456789 |
| B.—8th pt. 4 make 5 | 153456789 |
| C.—8th pt. 3 subjoin 6 | 1534(4+6)56789 |
| D.—8 is once; 8th pt. 2 subjoin 4 | 154296789 |
| E.—8 is once; 8th pt. 1 subjoin 2 | 154318789 |
| F.—8 is once | 154320789 |
| G.—8th pt. 7 make 8 and 6 | 1543208(8+6)9 |
| H.—8 is once; 8th pt. 6 make 7 and 4 | 15432097(9+4) |
| I.—8 is once | 154320985 |
If you divide the remainder 5, decimal 625 is obtained.
Where unoperated parts appear in parenthesis, the remark under G, Fig. 18, will similarly apply.
123456789 ÷ 9 = 13717421.
Fig. 21.
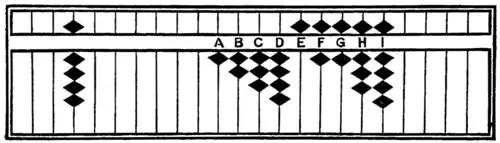
| A.—9th pt. 1 subjoin 1 | 163456789 |
| B.— 9th pt. 3 subjoin 3 | 136456789 |
| C.—9th pt. 6 subjoin 6 | 136(4+6)56789 |
| D.—9 is once; 9th pt. 1 subjoin 1 | 137166789 |
| E.—9th pt. 6 subjoin 6 | 13716(6+6)789 |
| F.—9 is once; 9th pt. 3 subjoin 3 | 137173(7+3)89 |
| G.—9 is once; 9th pt. 1 subjoin 1 | 137174199 |
| H.—9 is once | 137174209 |
| I.—9 is once | 13717421 |
No. 2.—It was already explained that the basis of division tables is 10; and, in going through the foregoing mono-divisions, you would find that, after division, unit is removed always one column higher in the quotient. For example:—in 6 ÷ 2 quotient 3 appears in the next higher column, and in 24 ÷ 3 quotient 8 appears in the original tens column.