Page:Euclid's Elements 1714 Barrow translation.djvu/34

This page has been proofread, but needs to be validated.

2. Caſe. If the baſe EF falls in the ſame place 1 9. ax.
 with EG,l it is evident that EG (BC) = EF.

3. Caſe. If EG fall below EF, then becauſe DG m 21. 1.
 + GEm = DF + FE, if from both DG, DF be taken away, which are equal, EG (BC) remains n 5. ax.
 n = EF. Which was to be demonstrated.

PROP. XXV.

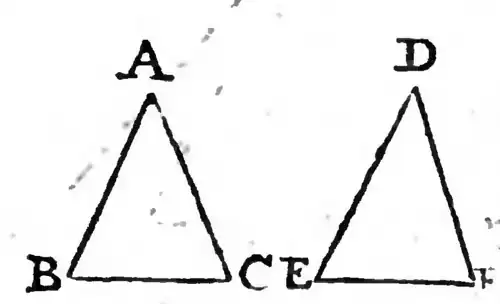
If two triangles ABC, DEF have two ſides AB, AC equal to two ſides DE, DF, each to other, and have the baſe BC greater than the bafe EF, they ſhall alſo have the angle A contained under the equal right lines greater than the angle D.

a 4. 1.
 For if the angle A be ſaid to be equal to D, a then is the baſe BC = EF, which is againſt the b 24. 1.
 Hypothesis. If it be ſaid the angle A > D,then b will be BC > EF, which is alfo againſt the Hyp. Therefore BC < EF. Which was to be dem.

PROP. XXVI.

If two triangles BAC, EDG have two angles of the one B, C equal to the two angles of the other E, DGE, each to his correſpondent angle, and have alſo one ſide of the one equal to one ſide of the other, either that ſide which lyeth betwixt the equal angles, or that which is ſubtended under one of the equal angles; the other ſidesalſo

This article is issued from Wikisource. The text is available under Creative Commons Attribution-Share Alike 4.0 unless otherwise noted. Additional terms may apply for the media files.