Page:EB1911 - Volume 27.djvu/290
(2) The two sides a, b and the included angle C being given, the angles A, B can be determined from the formulae A +B = π − C,
L tan 1/2 (A − B)=log (a−b)−log (a+b) + L cot 1/2C, and the side 1: is then obtained from the formula log c=log a+L sin C-L sin A.
(3) The two sides a, b and the angle A being given, the value of sin B may be found by means of the formula Lsin B=L sin A-Hog b-log a;
this gives two supplementary values of the angle B, if b sinA < a. If b sinA > athere is no solution, and if b sin A=a there is one solution. In the case b sin A < a, both values of B give solutions provided b > a, but the acute value only of B is admissible if b < a. The other side c can be then determined as in case (2). (4) If two angles A, B and a side a are given, the angle C is determined from the formula C=1r-A -B and the side b from the formula log b=log a-Q-L sin B-L sin A.
The area of a triangle is half the product of a side into the perpendicular from the opposite angle on that side; thus we obtain the expressions 1/2bc sin A, {s(s-a) (s-b)(s-c)}$ for the area of a triangle. A large collection of formulae for the area of a triangle are given in the Annals af Mathematics for X885 by M. Baker.
Let a, b, c, d denote the lengths of the sides AB, BC, CD, DA respectively of any plane quadrilateral and A+C=2a; we may obtain an expression for the area S of the quadrilateral in terms of the sides and the angle a.
We have 2S=ad sin A +bc sin(2a.-A) and $(a2+dz-b'-c ) =ad cos A -bc cos (aa.-A); hence 4S2+§ (a2+d2-b”-c2)'l=a2d'¢+b2c”-zabcd cos za. If 25 = a + b+c +d, the value of S may be written in the form S= {s(s-a)(s-b)(s-c)(s-d) -abcd cos2a}é. Let R denote the radius of the circumscribed circle, 1' of the inscribed, and ri, 72, ra of the escribed circles of a triangle Rad” °f CW" ABC; the values of these radii are given by the following formulae:-
”S;';"°db d R=abc/4S=a/2 sin A,
r=S/s ° r=S/s=(s-a)tan 5A =4R sin 1/2A sin 1/2B sin 1/2C r1=S/(5-a)=s tan 1/2A=4R sin 1/2A cos 1/2B cos 1/2C.
Spherical Trigonometry.
7. We shall throughout assume such elementary propositions in spherical geometry as are required for the purpose of the investigation of formulae given below.
A spherical triangle is the portion of the surface of a sphere bounded by three arcs of great circles of the sphere. If BC, CA, AB denote these arcs, the circular measure of the angles subtended by these arcs respectively at the centre of the sphere are the sides a, b, c of the spherical Definition of spherical Triangle. triangle ABC; and, if the portions of planes passing through these arcs and the centre of the sphere be drawn, the angles between the portions of planes intersecting at A, B, C respectively are the angles A, B, C of the spherical triangle. It is not necessary to consider triangles in which a side is greater than π, since we may replace such a side by the remaining arc of the great circle to Associated which it belongs. Since two great circles intersect »n Lmg, es each other in two points, there are eight triangles of which the sides are arcs of the same three great circles. If we consider one of these triangles ABC as the fundamental one, then one of the others is equal in all respects to ABC, and the remaining six have each one side equal to, or common with, a side of the triangle ABC, the opposite angle equal to the corresponding angle of ABC, and the other sides and angles supplementary to the corresponding sides and angles of ABC. These triangles may be called the associated triangles of the fundamental one ABC. It follows that from any general formula containing the sides and angles of a spherical triangle we may obtain other formulae by replacing two sides and the two angles opposite to them by their supplements, the remaining side and the remaining angle being unaltered, for such formulae are obtained by applying the given formulae to the associated triangles.
If A', , B', C' are those poles of the arcs BC, CA, AB respectively vx hich lie upon the same sides of them as the opposite angles A, B, C, then the triangle A'B'C' is called the polar triangle of the triangle ABC. The sides of the polar triangle are π-A, π−B, π−C, and the angles π−a, π−b, π−c. Hence from any general formula connecting the sides and angles of a spherical triangle we may obtain another formula by changing each side into the supplement of the opposite 0 Bangle and each angle into the supplement of the opposite side.

Fig. 5.
8. Let O be the centre of the sphere on which is the spherical triangle ABC. Draw AL perpendicular to OC and AM perpendicular to the plane OBC. Then the projection of OA on OB is the sum of the projections of OL, LM, MA on the same straight line. Since AM has no projection on any straight line in the plane OBC, this gives angles.
OA cos c=OL cos a+LM sin a.
Now OL=OA cos b, LM=AL cos C=OA sin b cos C;
therefore cos c =cos a cos b+sin a sin b cos C.
We may obtain similar formulae by interchanging the
letters a, b, c, thus
cos a=cos b cos c+sin b sin c cos A
cos b=cos c cos a+sin c sin a cos B (I) These formulae (I) may be regarded as the fundamental equations connecting the sides and angles of a spherical triangle; all the other relations which we shall give below may be deduced analytically from them; we shall, however, in most cases give independent proofs. By using the polar triangle transformation we have the formulae cos A = -cos B cos C+sin B sin C cos a cos B = -cos C cos A +sin C sin A cos b (2) cos C= -cos A cos B-i-sin A sin B cos 6 In the figures we have AM=AL sin Ci=r sin b sin C, where r denotes the radius of the sphere. By drawing a perpendicular from A on OB, we may in a similar manner show that A]lI= r sin c sin B,
By interchanging the sides we have the equation
we shall find below a symmetrical form for k. If we eliminate cos b between the first two formulae of (I) we have cos a sin2c=sin b sin c cos A +sin c cos c sin a cos B; therefore Cot a sin c = (sin b/sin a) cos A -f-cos c cos B =sin B cot A +cos c cos B.
We thus have the six equations
| cot a sin b =cot A sin C+cos b cos C | (4) | ||
| cot b sin a=cot B sin C+cos a cos C | |||
| cot b sin c =cot B sin A +cos c cos A | |||
| cot c sin b=cot C sin A +cos b cos A | |||
| cot c sin a=cot C sin B+cos a cos B | |||
| cot a sin c=cot A sin B+cos c cos B |
When C=1/2π formula (1) gives
cos c=cos a cos b (a)
and (3) gives sin b =sin B sin c ( sin a=sin A sin c B)
from (4) we get tan a =tan A sin, b=tan c cos B tan b =tan B sin a =tan c cos A (7) The formulae cos c =cot A cot B (e) and cos A -cos A sin B
cos c=cos a cos b+sin a sin b cos C
cos B=C0S b sin A ff)
follow at once from (a), (B),
used for the solution of
(v). These are the formulae which are right-angled triangles. Napier gave mnemonical rules for remembering them.
The following proposition follows easily from the theorem in equation (3): If AD, BE, CF are three arcs drawn through A, B, C to meet the opposite sides in D, E, F A respectively, and if these arcs pass through a point, the segments of the sides satisfy the relation sin BD sin CE sin AF=sin CD sin AE sin BF; and
conversely if this relation is satisfied the arcs pass through a point. From this theorem it follows that the three perpendiculars from the angles on the opposite sides, ' the three bisectors of
the angles, and the three arcs from
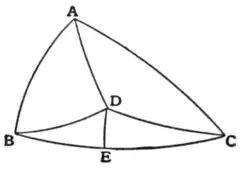
Fig. 6.
the angles to the middle points of the opposite sides each pass through a point.
Formula for Sine and Cosine of Half Angles.
9. If D be the point of intersection of the three bisectors of the angles A, B, C, and if DE be drawn perpendicular to BC, it may be shown that BE = § (a +C - b) and CE = § (a + b - C), and that the angles BDE, ADC are supplementary. We have sinADB sinb sinADC '-2 lA
also sinBD ' sin § A ' sin CD 'sin § A ' therefore Sm 2
- Sm BD Sm Sm. CDE Sm BDE. But sin BD sin BDE=sin BE
sin b sin c
=sin 1/2(a+c-b), and sin CD sin CDE=sin CE-=sin 1/2 (a+b-c); A ' l -b ' 1 b- 1 s
therefore sinA/2 {sin 1/2(a+c−b . . . (5)
Apply this formula to the associated triangle of which π−A, π−B, C are the angles and π−a, π−b, c are the sides; we obtain A jsin l(b+cf-a) sin 1(a+b+c)) the formula cos; - I- Sin b sin zc) 2 (6)