Calculus Made Easy/Chapter 5

In our equations we have regarded ${\displaystyle x}$ as growing, and as a result of ${\displaystyle x}$ being made to grow ${\displaystyle y}$ also changed its value and grew. We usually think of ${\displaystyle x}$ as a quantity that we can vary; and, regarding the variation of ${\displaystyle x}$ as a sort of cause, we consider the resulting variation of ${\displaystyle y}$ as an effect. In other words, we regard the value of ${\displaystyle y}$ as depending on that of ${\displaystyle x}$. Both ${\displaystyle x}$ and ${\displaystyle y}$ are variables, but ${\displaystyle x}$ is the one that we operate upon, and ${\displaystyle y}$ is the “dependent variable.” In all the preceding chapter we have been trying to find out rules for the proportion which the dependent variation in ${\displaystyle y}$ bears to the variation independently made in ${\displaystyle x}$.

Our next step is to find out what effect on the process of differentiating is caused by the presence of constants, that is, of numbers which don’t change when ${\displaystyle x}$ or ${\displaystyle y}$ change their values.

Added Constants.

Let us begin with some simple case of an added constant, thus:

Just as before, let us suppose ${\displaystyle x}$ to grow to ${\displaystyle x+dx}$ and ${\displaystyle y}$ to grow to ${\displaystyle y+dy}$.

Neglecting the small quantities of higher orders, this becomes

Subtract the original ${\displaystyle y=x^{3}+5}$, and we have left:

So the ${\displaystyle 5}$ has quite disappeared. It added nothing to the growth of ${\displaystyle x}$, and does not enter into the differential coefficient. If we had put ${\displaystyle 7}$, or ${\displaystyle 700}$, or any other number, instead of ${\displaystyle 5}$, it would have disappeared. So if we take the letter ${\displaystyle a}$, or ${\displaystyle b}$, or ${\displaystyle c}$ to represent any constant, it will simply disappear when we differentiate.

If the additional constant had been of negative value, such as ${\displaystyle -5}$ or ${\displaystyle -b}$, it would equally have disappeared.

Multiplied Constants.

Take as a simple experiment this case:

Let ${\displaystyle y=7x^{2}}$.

Then on proceeding as before we get:

Then, subtracting the original ${\displaystyle y=7x^{2}}$, and neglecting the last term, we have

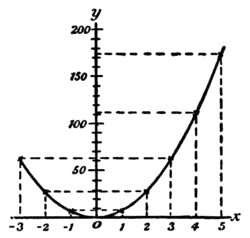
​Let us illustrate this example by working out the graphs of the equations ${\displaystyle y=7x^{2}}$ and ${\displaystyle {\frac {dy}{dx}}=14x}$, by assigning to ${\displaystyle x}$ a set of successive values, ${\displaystyle 0,1,2,3,}$ etc., and finding the corresponding values of ${\displaystyle y}$ and of ${\displaystyle {\frac {dy}{dx}}}$.

These values we tabulate as follows:

${\displaystyle x}$	${\displaystyle 0}$	${\displaystyle 1}$	${\displaystyle 2}$	${\displaystyle 3}$	${\displaystyle 4}$	${\displaystyle 5}$	${\displaystyle -1}$	${\displaystyle -2}$	${\displaystyle -3}$
${\displaystyle y}$	${\displaystyle 0}$	${\displaystyle 7}$	${\displaystyle 28}$	${\displaystyle 63}$	${\displaystyle 112}$	${\displaystyle 175}$	${\displaystyle 7}$	${\displaystyle 28}$	${\displaystyle 63}$
${\displaystyle {\tfrac {dy}{dx}}}$	${\displaystyle 0}$	${\displaystyle 14}$	${\displaystyle 28}$	${\displaystyle 42}$	${\displaystyle 56}$	${\displaystyle 70}$	${\displaystyle -14}$	${\displaystyle -28}$	${\displaystyle -42}$

Fig. 6.—Graph of ${\displaystyle y=7x^{2}}$.	Fig. 6a.—Graph of ${\displaystyle {\frac {dy}{dx}}=14x}$.

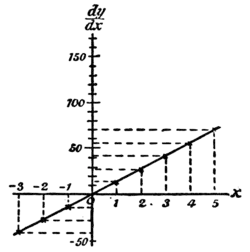
Now plot these values to some convenient scale, and we obtain the two curves, Fig. 6 and 6a.

​Carefully compare the two figures, and verify by inspection that the height of the ordinate of the derived curve, Fig. 6a, is proportional to the slope of the original curve,^[1] Fig. 6, at the corresponding value of ${\displaystyle x}$. To the left of the origin, where the original curve slopes negatively (that is, downward from left to right) the corresponding ordinates of the derived curve are negative.

Now if we look back at p. 19, we shall see that simply differentiating ${\displaystyle x^{2}}$ gives us ${\displaystyle 2x}$. So that the differential coefficient of ${\displaystyle 7x^{2}}$ is just ${\displaystyle 7}$ times as big as that of ${\displaystyle x^{2}}$. If we had taken ${\displaystyle 8x^{2}}$, the differential coefficient would have come out eight times as great as that of ${\displaystyle x^{2}}$. If we put ${\displaystyle y=ax^{2}}$, we shall get

If we had begun with ${\displaystyle y=ax^{n}}$, we should have had ${\displaystyle {\frac {dy}{dx}}=a\times nx^{n-1}}$. So that any mere multiplication by a constant reappears as a mere multiplication when the thing is differentiated. And, what is true about multiplication is equally true about division: for if, in the example above, we had taken as the constant ${\displaystyle {\tfrac {1}{7}}}$ instead of ${\displaystyle 7}$, we should have had the same ${\displaystyle {\tfrac {1}{7}}}$ come out in the result after differentiation.

​Some Further Examples.

The following further examples, fully worked out, will enable you to master completely the process of differentiation as applied to ordinary algebraical expressions, and enable you to work out by yourself the examples given at the end of this chapter.

(1) Differentiate ${\displaystyle y={\frac {x^{5}}{7}}-{\frac {3}{5}}}$.

${\displaystyle {\frac {3}{5}}}$ is an added constant and vanishes (see p. 26).

We may then write at once

or

(2) Differentiate ${\displaystyle y=a{\sqrt {x}}-{\frac {1}{2}}{\sqrt {a}}}$.

The term ${\displaystyle {\frac {1}{2}}{\sqrt {a}}}$ vanishes, being an added constant; and as ${\displaystyle a{\sqrt {x}}}$, in the index form, is written ${\displaystyle ax^{\frac {1}{2}}}$, we have

or

(3) If ${\displaystyle ay+bx=by-ax+(x+y){\sqrt {a^{2}-b^{2}}}}$, find the differential coefficient of ${\displaystyle y}$ with respect to ${\displaystyle x}$.

As a rule an expression of this kind will need a little more knowledge than we have acquired so far; ​it is, however, always worth while to try whether the expression can be put in a simpler form.

First we must try to bring it into the form ${\displaystyle y=}$ some expression involving ${\displaystyle x}$ only.

The expression may be written

Squaring, we get

which simplifies to

or

that is

hence ${\displaystyle y={\sqrt {\frac {a+b}{a-b}}}x}$ and ${\displaystyle {\frac {dy}{dx}}={\sqrt {\frac {a+b}{a-b}}}}$.

(4) The volume of a cylinder of radius ${\displaystyle r}$ and height ${\displaystyle h}$ is given by the formula ${\displaystyle V=\pi r^{2}h}$. Find the rate of variation of volume with the radius when ${\displaystyle r=5.5}$ in. and ${\displaystyle h=20}$ in. If ${\displaystyle r=h}$, find the dimensions of the cylinder so that a change of ${\displaystyle 1}$ in. in radius causes a change of ${\displaystyle 400}$ cub. in. in the volume.

The rate of variation of ${\displaystyle V}$ with regard to ${\displaystyle r}$ is

If ${\displaystyle r=5.5}$ in. and ${\displaystyle h=20}$ in. this becomes ${\displaystyle 690.8}$. It means that a change of radius of ${\displaystyle 1}$ inch will cause a change of volume of ${\displaystyle 690.8}$ cub. inch. This can be easily verified, for the volumes with ${\displaystyle r=5}$ and ${\displaystyle r=6}$ ​are ${\displaystyle 1570}$ cub. in. and ${\displaystyle 2260.8}$ cub. in. respectively, and ${\displaystyle 2260.8-1570=690.8}$.

Also, if

(5) The reading ${\displaystyle \theta }$ of a Féry’s Radiation pyrometer is related to the Centigrade temperature ${\displaystyle t}$ of the observed body by the relation

where ${\displaystyle {\theta _{1}}}$ is the reading corresponding to a known temperature ${\displaystyle t_{1}}$ of the observed body.

Compare the sensitiveness of the pyrometer at temperatures ${\displaystyle 800^{\circ }}$C., ${\displaystyle 1000^{\circ }}$C., ${\displaystyle 1200^{\circ }}$C., given that it read ${\displaystyle 25}$ when the temperature was ${\displaystyle 1000^{\circ }}$C.

The sensitiveness is the rate of variation of the reading with the temperature, that is ${\displaystyle {\frac {d\theta }{dt}}}$. The formula may be written

and we have

When ${\displaystyle t=800}$, ${\displaystyle 1000}$ and ${\displaystyle 1200}$, we get ${\displaystyle {\frac {d\theta }{dt}}=0.0512}$, ${\displaystyle 0.1}$ and ${\displaystyle 0.1728}$ respectively.

The sensitiveness is approximately doubled from ${\displaystyle 800^{\circ }}$ to ${\displaystyle 1000^{\circ }}$, and becomes three-quarters as great again up to ${\displaystyle 1200^{\circ }}$.

​Exercises II. (See p. 254 for Answers.)

Differentiate the following:

(1) ${\displaystyle y=ax^{3}+6}$.	(2) ${\displaystyle y=13x^{\tfrac {3}{2}}-c}$.
(3) ${\displaystyle y=12x^{\tfrac {1}{2}}+c^{\tfrac {1}{2}}}$.	(4) ${\displaystyle y=c^{\tfrac {1}{2}}x^{\tfrac {1}{2}}}$.
(5) ${\displaystyle u={\frac {az^{n}-1}{c}}}$.	(6) ${\displaystyle y=1.18t^{2}+22.4}$.

Make up some other examples for yourself, and try your hand at differentiating them.

(7) If ${\displaystyle l_{t}}$ and ${\displaystyle l_{0}}$ be the lengths of a rod of iron at the temperatures ${\displaystyle t^{\circ }}$ C. and ${\displaystyle 0^{\circ }}$ C. respectively, then ${\displaystyle l_{t}=l_{0}(1+0.000012t)}$. Find the change of length of the rod per degree Centigrade.

(8) It has been found that if ${\displaystyle c}$ be the candle power of an incandescent electric lamp, and ${\displaystyle V}$ be the voltage, ${\displaystyle c=aV^{b}}$, where ${\displaystyle a}$ and ${\displaystyle b}$ are constants.

Find the rate of change of the candle power with the voltage, and calculate the change of candle power per volt at ${\displaystyle 80}$, ${\displaystyle 100}$ and ${\displaystyle 120}$ volts in the case of a lamp for which ${\displaystyle a=0.5\times 10^{-10}}$ and ${\displaystyle b=6}$.

(9) The frequency ${\displaystyle n}$ of vibration of a string of diameter ${\displaystyle D}$, length ${\displaystyle L}$ and specific gravity ${\displaystyle \sigma }$, stretched with a force ${\displaystyle T}$, is given by

Find the rate of change of the frequency when ${\displaystyle D}$, ${\displaystyle L}$, ${\displaystyle \sigma }$ and ${\displaystyle T}$ are varied singly. ​(10) The greatest external pressure ${\displaystyle P}$ which a tube can support without collapsing is given by

where ${\displaystyle E}$ and ${\displaystyle \sigma }$ are constants, ${\displaystyle t}$ is the thickness of the tube and ${\displaystyle D}$ is its diameter. (This formula assumes that ${\displaystyle 4t}$ is small compared to ${\displaystyle D}$.)

Compare the rate at which ${\displaystyle P}$ varies for a small change of thickness and for a small change of diameter taking place separately.

(11) Find, from first principles, the rate at which the following vary with respect to a change in radius:

(a) the circumference of a circle of radius ${\displaystyle r}$;

(b) the area of a circle of radius ${\displaystyle r}$;

(c) the lateral area of a cone of slant dimension ${\displaystyle l}$;

(d) the volume of a cone of radius ${\displaystyle r}$ and height ${\displaystyle h}$;

(e) the area of a sphere of radius ${\displaystyle r}$;

(f) the volume of a sphere of radius ${\displaystyle r}$.

(12) The length ${\displaystyle L}$ of an iron rod at the temperature ${\displaystyle T}$ being given by ${\displaystyle L=l_{t}\left[1+0.000012(T-t)\right]}$, where ${\displaystyle l_{t}}$ is the length at the temperature ${\displaystyle t}$, find the rate of variation of the diameter ${\displaystyle D}$ of an iron tyre suitable for being shrunk on a wheel, when the temperature ${\displaystyle T}$ varies.